LISTA DE EXERCÍCIOS - CICLO 3 - CADERNO 5
1) Um carro de 800 kg andando a 108 km/h, freia bruscamente e pára em 5,0s.
a) Qual é a aceleração do carro? b) Qual o valor da força de
atrito que atua sobre o carro?
2) (FUVEST) O sistema indicado na figura a seguir, onde
as polias são ideais, permanece em repouso graças à força de atrito entre o
corpo de 10 kg e a superfície de apoio. Podemos afirmar que o valor da força de
atrito é:
a) 20 N
b) 10 N c) 100 N d) 60 N
e) 40 N
3) (FUVEST) Tenta-se, sem sucesso, deslocar
uma caixa de peso P = 50 N, em repouso sobre um plano horizontal com atrito,
aplicando-lhe uma força
F = 200 N, na direção da haste. Despreze a
massa da haste.
a) Faça um esquema de todas as
forças que agem sobre a caixa e identifique claramente a origem de cada uma
delas. Escreva o valor, em N, da resultante dessas forças (FR).
b) Qual o valor da força de atrito
entre a caixa e o plano (em N)?
c) Qual o valor mínimo do
coeficiente de atrito?
4) (UFMG) Nessa figura,
está representado um bloco de 2,0 kg sendo pressionado contra a parede por uma
força μ O coeficiente de atrito estático entre esses corpos vale 0,5, e o
cinético vale 0,3. Considere g = 10 m/s2.
Se F = 50 N, então a reação normal
e a força de atrito que atuam sobre o bloco valem, respectivamente,
a) 20 N e 6,0 N b) 20 N e 10 N c)
50 N e 20 N. d) 50 N e 25 N. e)
70 N e 35 N.
5) (UNESP) No sistema a
seguir, A tem massa mA = 10 kg. B tem massa mB = 15 kg. α
= 45°.
Qual será o coeficiente de atrito
entre as superfícies em contato, do corpo A com o plano, para que o corpo se
desloque com movimento uniforme?
Observações: g = 10 m/s2;
o peso da corda, o atrito no eixo da roldana e a massa da roldana são
desprezíveis.
6) (UNESP) A figura ilustra
um jovem arrastando um caixote com uma corda, ao longo de uma superfície
horizontal, com velocidade constante. A tração (T vetorial) que ele exerce no
fio é de 20 N.
a) Desenhe todas as forças que
atuam sobre o caixote, nomeando-as.
b) Calcule a força de atrito entre
o caixote e o solo. São dados:
sen 37° = cos 53° = 0,6; sen 53° =
cos 37° = 0,8.
7) (UNESP) Um bloco de massa m = 5,0 kg está apoiado sobre um
plano, inclinado de 30° em relação à horizontal. Se uma força F, paralela ao
plano inclinado, é aplicada ao bloco com sentido para cima, o bloco desliza
para baixo com velocidade v = (2t) m/s. Se a mesma força F é aplicada para
baixo, o corpo desliza com velocidade v' = (3t) m/s.
a) Calcule F.
b) Calcule o coeficiente de atrito
de deslizamento entre o corpo e o plano inclinado.
8) (UNIRIO) Um carro é
freado, e suas rodas, travadas ao descer uma rampa. Num dia seco, o carro pára
antes do final da descida. Num dia chuvoso, isto ocorrerá se:
a) Fat < P sen
Ɵ, em qualquer circunstância.
b) Fat < P sen
Ɵ, dependendo do local onde se inicia a freada e da velocidade naquele
instante.
c) Fat = P sen Ɵ,
em qualquer circunstância.
d) Fat = P sen Ɵ,
dependendo do local onde se inicia a freada e da velocidade naquele instante.
e) Fat > P sen
Ɵ, dependendo do local onde se inicia a freada e da velocidade naquele instante.
9) (FUVEST) Considere o
movimento de uma bola abandonada em um plano inclinado no instante t = 0.
O par de gráficos
que melhor representa, respectivamente, a velocidade (em módulo) e a distância
percorrida, é: a) II e IV b) IV e III c) III e II d) I e II
e) I e IV
10) (MACKENZIE) Num local onde a
aceleração gravitacional tem módulo 10 m/s2, dispõe-se o conjunto a
seguir, no qual o atrito é desprezível, a polia e o fio são ideais. Nestas
condições, a intensidade da força que o bloco A exerce no bloco B é: a) 20 N b) 32
N c) 36 N
d) 72 N e) 80 N
Dados: m (A) = 6,0 kg m (B) = 4,0
kg m (C) = 10 kg cos α = 0,8
sen α= 0,6
11) (MACKENZIE) A ilustração a
seguir refere-se a uma certa tarefa na qual o bloco B dez vezes mais pesado que
o bloco A deverá descer pelo plano inclinado com velocidade constante. Considerando
que o fio e a polia são ideais, o coeficiente de atrito cinético entre o bloco
B e o plano deverá ser: a) 0,500 b) 0,750
c) 0,875 d) 1,33 e) 1,50 Dados: sen α= 0,6 cos α = 0,8
12) (MACKENZIE) Os corpos A e B,
de massas 8 kg e 2 kg, respectivamente, sobem o plano inclinado a seguir com
aceleração constante de 1 m/s2. Se o coeficiente de atrito cinético
entre os blocos e o plano inclinado é 0,5, então o módulo da força F, paralela
ao apoio dos blocos e no plano da figura, vale:
a) 140 N b) 130 N c) 120 N
d) 110 N e) 100 N
13) (MACKENZIE) Um bloco de 10kg
repousa sozinho sobre o plano inclinado a seguir. Esse bloco se desloca para
cima, quando se suspende em P‚ um corpo de massa superior a 13,2kg.
Retirando-se o corpo de P2, a maior massa que poderemos suspender em
P para que o bloco continue em repouso, supondo os fios e as polias ideais,
deverá ser de: a) 1,20 kg b) 1,32 kg
c) 2,40 kg d) 12,0 kg e) 13,2 kg
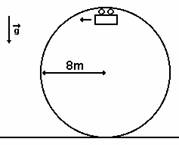
14) (FUVEST) A figura a seguir
mostra, num plano vertical, parte dos trilhos do percurso circular de uma
"montanha russa" de um parque de diversões. A velocidade mínima que o
carrinho deve ter, ao passar pelo ponto mais alto da trajetória, para não
desgrudar dos trilhos vale, em metros por segundos:
a) √20. b) √40.
c) √80. d) √160. e)
√320.
15) (UEL) Num pêndulo
cônico, a massa m gira numa circunferência horizontal, estando submetida às
forças peso P vetorial e tração T vetorial, conforme a figura a seguir.
Nestas condições, a intensidade da
força centrípeta é
a) nula, pois o movimento é
uniforme.
b) dada pela componente da tração,
T.senƟ
c) dada pela componente da tração,
T.cosƟ
d) dada pela resultante T - P cosƟ
e) dada pela resultante T - P senƟ
16) (UNESP) Um cubo de aço e outro de cobre, ambos de massas
iguais a 20 g estão sobre um disco de aço horizontal, que pode girar em torno
de seu centro. Os coeficientes de atrito estático para aço-aço e cobre-aço são,
respectivamente, μA = 0,74 e μB = 0,53. O cubo de cobre
está inicialmente a uma distância de 10 cm do centro do disco. Aceleração da
gravidade = 10 m/s2.
a) Qual deve ser a velocidade
angular do disco para que o cubo de cobre comece a deslizar?
b) A que distância do centro deve
estar o cubo de aço para que o seu deslizamento seja simultâneo com o de cobre?
17) (UNICAMP) Uma criança de 15
kg está sentada em um balanço sustentado por duas cordas de 3,0 m de
comprimento cada, conforme mostram as figuras (a) e (b) a seguir.
a) Qual a tensão em cada uma das
duas cordas quando o balanço está parado figura (a)?
b) A criança passa a balançar de
modo que o balanço atinge 0,5 m de altura em relação ao seu nível mais baixo,
figura (b). Qual a tensão máxima em cada uma das duas cordas nesta situação?
18) (MACKENZIE) Um corpo de pequenas
dimensões realiza voltas verticais no sentido horário dentro de uma esfera
rígida de raio R = 1,8 m. Na figura a seguir, temos registrado o instante em
que sua velocidade é 6,0 m/s e a força de atrito devido ao contato com a esfera
é equilibrada pelo peso. Nestas condições, o coeficiente de atrito cinético
entre o corpo e a esfera é: a) 0,10 b)
0,20 c) 0,30 d) 0,40
e) 0,50
Adote :g = 10 m/s2
19) (UNICAMP) Sob a ação de uma força constante, um corpo de massa
m = 4,0 kg adquire, a partir do repouso, a velocidade de 10 m/s.
a) Qual é o trabalho realizado por
essa força?
b) Se o corpo se deslocou 25 m,
qual o valor da força aplicada?
20) (UNICAMP) Uma criança solta
uma pedrinha de massa m = 50 g, com velocidade inicial nula, do alto de um
prédio de 100 m de altura. Devido ao atrito com o ar, o gráfico da posição da
pedrinha em função do tempo não é mais a parábola y = 100 - 5t2, mas
sim o gráfico representado adiante,
a) Com que velocidade a pedrinha
bate no chão (altura = 0)?
b) Qual é o trabalho realizado
pela força de atrito entre t = 0 e t = 11 segundos?
21) (UNICAMP) A figura a seguir
representa uma certa fibra óptica que consiste de um núcleo cilíndrico de
índice de reflexão n > 1, circundado por ar cujo índice vale 1,0. Se o ângulo
α representado na figura for suficientemente grande, toda a luz será refletida
em ziguezague nas paredes do núcleo, sendo assim guiada e transmitida por
longas distâncias. No final da fibra a luz sai para o ar formando um cone de
ângulo ϕ, conforme a figura.
a) Qual o valor mínimo de sen α em
termos de n para que a luz seja guiada?
b) Qual o valor de sen ϕ em termos
de n?
22) (UNESP) A figura adiante
mostra, esquematicamente, o comportamento de um raio de luz que atinge um
dispositivo de sinalização instalado numa estrada, semelhante ao conhecido
"olho-de-gato".
De acordo com a figura responda:
a) Que fenômenos ópticos ocorrem
nos pontos I e II?
b) Que relação de desigualdade
deve satisfazer o índice de refração do plástico para que o dispositivo opere
adequadamente, conforme indicado na figura?
23) (UNESP) A figura a seguir mostra um raio de
luz monocromática propagando-se no ar e atingindo o ponto A da superfície de um
paralelepípedo retângulo feito de vidro transparente. A linha pontilhada, normal
à superfície no ponto de incidência do raio luminoso, e os três raios
representados estão situados num mesmo plano paralelo a uma das faces do bloco.
a) De acordo com a figura, que
fenômenos estão ocorrendo no ponto A?
b) O ângulo limite para um raio da
luz considerada, quando se propaga desse vidro para o ar, é 42°. Mostre o que
acontecerá com o raio no interior do vidro ao atingir o ponto B.
24) (UFSCAR) O prisma da
figura está colocado no ar e o material de que é feito tem um índice de
refração igual a √2. Os ângulos A são iguais a 30°. Considere dois raios de luz
incidentes perpendiculares à face maior.
a) Calcule o ângulo com que os
raios emergem do prisma.
b) Qual deve ser o índice de
refração do material do prisma para que haja reflexão total nas faces OA?
25) (UNICAMP) Um sistema de
lentes produz a imagem real de um objeto, conforme a figura a seguir. Calcule a
distância focal e localize a posição de uma lente delgada que produza o mesmo
efeito.
26) (UNESP) Uma lente delgada, convergente, tem distância focal
f. Um feixe de raios paralelos ao eixo da lente incide sobre esta. No espaço
imagem é colocado um espelho paralelo à lente, que intercepta os raios
emergentes dela.
a) Desenhe um esquema do problema
proposto.
b) A que distância da lente (em
função de f) deve ser colocado o espelho, para que o foco imagem se posicione
no ponto intermediário entre a lente e o espelho?
27) (UFRRJ) A figura mostra
dois raios luminosos que incidem sobre uma lente, formando um ângulo de 30° com
a normal a ela e emergindo paralelos. A distância entre os pontos A e B em que
os raios atingem a lente é de 20 cm. Determine
a distância focal da lente.
28) (UNIFESP) Considere as situações seguintes.
I. Você vê a imagem ampliada do
seu rosto, conjugada por um espelho esférico.
II. Um motorista vê a imagem
reduzida de um carro atrás do seu, conjugada pelo espelho retrovisor direito.
III. Uma aluna projeta, por meio
de uma lente, a imagem do lustre do teto da sala de aula sobre o tampo da sua
carteira.
A respeito dessas imagens, em
relação aos dispositivos ópticos referidos, pode-se afirmar que
a) as três são virtuais b) I e II são virtuais; III é
real
c) I é virtual; II e III são
reais d) I é
real; II e III são virtuais e) as três são reais.
29) (MACKENZIE) Uma lente delgada
convergente tem distância focal de 20 cm. Para se obter uma imagem conjugada de
um objeto real, maior que o próprio objeto e não invertida, esse deverá ser
colocado sobre o eixo principal da lente, a) a 40 cm do centro óptico b) a 20 cm do centro óptico c) a mais de 40 cm do centro
óptico d) entre 20 cm e 40 cm do
centro óptico e) a menos de
20 cm do centro óptico
30) (UFF) Observe
atentamente a fotografia do grafite:
A lente objetiva
usada para tirar a fotografia do grafite pode ser considerada como uma lente
convergente delgada. Chame de p a distância entre a objetiva e a parede
fotografada, de d a distância entre a objetiva e o plano do filme fotográfico
(ou célula CCD numa câmera digital), e de f a distância focal da objetiva.
Assinale a opção que identifica
corretamente, para a situação da fotografia mencionada, como estão relacionadas
as 3 distâncias p, d e f e qual a orientação da imagem formada sobre o filme.
a) p > f > d; imagem
invertida b) d > f
> p; imagem direita
c) p > d > f; imagem
invertida d) f > d
> p; imagem direita
e) d > p > f; imagem
invertida
31) (UNESP) Uma lupa
utilizada para leitura é confeccionada com uma lente delgada convergente,
caracterizada por uma distância focal f. Um objeto é colocado a uma distância
0,8 f, medida a partir da lente. Se uma letra de um texto tem altura 1,6 mm,
determine o tamanho da letra observado pelo leitor.
32) (FATEC) Sobre uma mesa,
são colocados alinhados uma vela acesa, uma lente convergente e um alvo de
papel.
Inicialmente, a
vela é afastada da lente tanto quanto possível, e ajusta-se a posição do alvo
para se obter nele a imagem mínima da vela. Mede-se e anota-se a distância f do
alvo à lente. Aproximando-se a vela, até que fique à distância (3/2) f da
lente, para captar imagem nítida da vela o alvo deverá ser posicionado à
distância da lente igual a
a) 2/3 f b) f c) 3/2 f d) 2 f e) 3 f
33) (PUC) Certo professor
de física deseja ensinar a identificar três tipos de defeitos visuais apenas
observando a imagem formada através dos óculos de seus alunos, que estão na
fase da adolescência. Ao observar um objeto através do primeiro par de óculos,
a imagem aparece diminuída. O mesmo objeto observado pelo segundo par de óculos
parece aumentado e apenas o terceiro par de óculos distorce as linhas quando
girado.
Através da análise das imagens
produzidas por esses óculos podemos concluir que seus donos possuem,
respectivamente:
a) Miopia, astigmatismo e
hipermetropia.
b) Astigmatismo, miopia e
hipermetropia.
c) Hipermetropia, miopia e
astigmatismo.
d) Hipermetropia, astigmatismo e
miopia.
e) Miopia, hipermetropia e astigmatismo.
34) (UFPA) Um oftalmologista, antes de examinar um paciente,
explica-lhe dois defeitos da visão usando os esquemas da Figura 1.
Em seguida, mostra-lhe as lentes
representadas na Figura 2, cuja função é corrigir esses defeitos.
a) Qual o nome de cada defeito e
qual a lente (1 ou 2) que corrige cada um?
b) Após o exame, o médico constata
que o olho do paciente apresenta o defeito A, sendo sua máxima distância de
visão distinta igual a 50 cm. Calcule quantas dioptrias deve ter a lente
receitada pelo médico para corrigir tal defeito.
35) (UFSCAR) Pesquisas recentes mostraram que o cristalino humano
cresce durante a vida, aumentando seu diâmetro cerca de 0,02 mm por ano. Isso
acarreta, na fase de envelhecimento, um defeito de visão chamado presbiopia,
que pode ser corrigido de forma semelhante
a) à miopia, com uso de lentes
divergentes.
b) à miopia, com uso de lentes
convergentes.
c) à hipermetropia, com uso de
lentes divergentes.
d) à hipermetropia, com uso de
lentes convergentes.
e) ao astigmatismo, com uso de
lentes convergentes ou divergentes.
36) (UNICAMP) O olho humano só
é capaz de focalizar a imagem de um objeto (fazer com que ela se forme na
retina) se a distância entre o objeto e o cristalino do olho for maior que a de
um ponto conhecido como ponto próximo, Pp (ver figura adiante). A posição do
ponto próximo normalmente varia com a idade. Uma pessoa, aos 25 anos,
descobriu, com auxílio do seu oculista, que o seu ponto próximo ficava a 20 cm
do cristalino. Repetiu o exame aos 65 anos e constatou que só conseguia
visualizar com nitidez objetos que ficavam a uma distância mínima de 50 cm.
Considere que para essa pessoa a retina está sempre a 2,5 cm do cristalino,
sendo que este funciona como uma lente convergente de distância focal variável.
a) Calcule as distâncias focais
mínimas do cristalino dessa pessoa aos 25 e aos 65 anos.
b) Se essa pessoa, aos 65 anos,
tentar focalizar um objeto a 20 cm do olho, a que distância da retina se
formará a imagem?
37) (UNIFESP) Uma das lentes dos óculos de uma pessoa tem
convergência +2,0 di. Sabendo que a distância mínima de visão distinta de um
olho normal é 0,25 m, pode-se supor que o defeito de visão de um dos olhos
dessa pessoa é
a) hipermetropia, e a distância
mínima de visão distinta desse olho é 40 cm.
b) miopia, e a distância máxima de
visão distinta desse olho é 20 cm.
c) hipermetropia, e a distância
mínima de visão distinta desse olho é 50 cm.
d) miopia, e a distância máxima de
visão distinta desse olho é 10 cm.
e) hipermetropia, e a distância mínima
de visão distinta desse olho é 80 cm.
38) (FGV) Quando uma onda eletromagnética se propaga em um meio
material, alguns fatores devem ser levados em conta. Analise-os.
I - No vácuo, a luz vermelha e a
verde apresentam mesmas velocidades, porém, na água, suas velocidades ficam
diferentes.
II - A direção de propagação das
ondas eletromagnéticas é transversal à direção da vibração da fonte que as
produz, independentemente do meio que essas ondas atravessam.
III - Nos meios materiais, desde
que uma onda eletromagnética possa se propagar, a velocidade de propagação
depende da frequência.
É CORRETO o contido em:
a) I, apenas b) II, apenas c) I e III, apenas d) II e III, apenas e) I, II e III
39) (UFSCAR) A diferença entre ondas mecânicas, como o som, e
eletromagnéticas, como a luz, consiste no fato de que
a) a velocidade de propagação,
calculada pelo produto do comprimento de onda pela freqüência, só é assim
obtida para ondas eletromagnéticas.
b) as ondas eletromagnéticas podem
assumir uma configuração mista de propagação transversal e longitudinal.
c) apenas as ondas
eletromagnéticas, em especial a luz, sofrem o fenômeno denominado difração.
d) somente as ondas
eletromagnéticas podem propagar-se em meios materiais ou não materiais.
e) a interferência é um fenômeno
que ocorre apenas com as ondas eletromagnéticas
40) (UNIFESP) Na região
quadriculada da figura existe um campo magnético uniforme, perpendicular ao
plano do reticulado e penetrando no plano da figura. Parte de um circuito
rígido também passa por ela, como ilustrado na figura.
A aresta de cada
célula quadrada do quadrilátero tem comprimento u, e pelo fio passa uma
corrente elétrica de intensidade i. Analisando a força magnética que age sobre
cada elemento de comprimento u do fio do circuito, coincidente com a aresta das
células quadradas, a intensidade da força magnética resultante sobre a parte do
circuito exposta ao campo B é: a)
nula b) iBu/2 c) iBu d) 3iBu e) 13iBu
41) (UEG) A figura a seguir
descreve uma regra, conhecida como "regra da mão direita", para
análise da direção e do sentido do vetor campo magnético em torno de um fio
percorrido por uma corrente elétrica.
Analisando a figura a seguir,
responda aos itens:
a) O que representam, na figura,
as setas que estão ao lado dos dedos polegar e indicador?
b) Faça um esboço (desenho) das
linhas de campo magnético em torno desse fio.
c) Faça uma análise qualitativa
relacionando a dependência do módulo do vetor campo magnético nas proximidades
do fio com a intensidade de corrente elétrica e com a distância em que se
encontra do fio.
42) (UEG) Como se tivessem uma bússola natural, os pássaros que
migram são capazes de aproveitar o campo magnético da Terra para manter o curso
correto durante longos vôos. Os cientistas não sabem ao certo como isso
funciona, mas estudos recentes mostram que eles seriam dotados de um tipo de
sinestesia e estariam aptos a "ver" as linhas de campo magnético como
padrões de cores e luz.
"GALILEU",
São Paulo, abr. 2007, p. 31. [Adaptado].
Com respeito ao texto acima e
acerca dos conceitos de linhas de indução magnética, é INCORRETO afirmar:
a) As linhas de indução de um
campo magnético partem do Pólo Norte e dirigem-se para o Pólo Sul magnético.
b) As linhas de indução do campo
magnético de um condutor reto, percorrido por uma corrente elétrica, são
elipses concêntricas com o condutor, situadas em planos perpendiculares a ele.
c) O vetor indução magnética
gerado por uma espira circular percorrida por uma corrente elétrica é
perpendicular ao plano definido por ela.
d) No interior de um solenóide, em
pontos não muito próximos do fio condutor ou das extremidades, as linhas de
indução são representadas aproximadamente por retas igualmente espaçadas e
igualmente orientadas.
43) (UFMG) O Professor Nogueira montou, para seus alunos, a
demonstração de magnetismo que se descreve a seguir e que está representada na
Figura I.
Uma barra cilíndrica, condutora,
horizontal, está pendurada em um suporte por meio de dois fios condutores
ligados às suas extremidades. Esses dois fios são ligados eletricamente aos
pólos de uma bateria.
Em um trecho de comprimento L
dessa barra, atua um campo magnético B, vertical e uniforme. O módulo do campo
magnético é de 0,030 T, o comprimento L = 0,60 m e a corrente elétrica na barra
é de 2,0 A.
Despreze a massa dos fios.
Nessas circunstâncias, a barra
fica em equilíbrio quando os fios de sustentação estão inclinados 30° em
relação à vertical.
Na Figura II, está representada a
mesma barra, agora vista em perfil, com a corrente elétrica entrando na barra,
no plano do papel.
a) Considerando
essas informações, ESBOCE, na Figura II, o diagrama das forças que atuam na
barra e IDENTIFIQUE os agentes que exercem cada uma dessas forças.
b) DETERMINE a massa da barra.
44) (UFMG) Em uma aula de
eletromagnetismo, o Professor Emanuel faz a montagem mostrada,
esquematicamente, nesta figura:
Nessa montagem, uma barra de metal
não-magnético está em contato elétrico com dois trilhos metálicos paralelos e
pode deslizar sobre eles, sem atrito. Esses trilhos estão fixos sobre uma mesa
horizontal, em uma região onde há um campo magnético uniforme, vertical e para
baixo, que está indicado, na figura, pelo símbolo X. Os trilhos são ligados em
série a um amperímetro e a um resistor R. Considere que, inicialmente, a barra
está em repouso. Em certo momento, Emanuel empurra a barra no sentido indicado
pela seta e, em seguida, solta-a. Nessa situação, ele observa uma corrente
elétrica no amperímetro.
Com base nessas informações,
a) INDIQUE, na figura, o sentido
da corrente elétrica observada por Emanuel. JUSTIFIQUE sua resposta.
b) RESPONDA:
Após a barra ser solta, sua
velocidade DIMINUI, PERMANECE CONSTANTE ou AUMENTA com o tempo? JUSTIFIQUE
sua resposta.
45) (PUCRIO) Dois objetos metálicos esféricos idênticos, contendo
cargas elétricas de 1 C e de 5 C, são colocados em contato e depois afastados a
uma distância de 3 m. Considerando a Constante de Coulomb k = 9 × 109
N m2/C2, podemos dizer que a força que atua entre as
cargas após o contato é:
a) atrativa e tem módulo 3 ×109
N.
b) atrativa e tem módulo 9 × 109
N.
c) repulsiva e tem módulo 3 × 109N.
d) repulsiva e tem módulo 9 × 109
N.
e) zero.
46) (FUVEST) Duas barras
isolantes, A e B, iguais, colocadas sobre uma mesa, têm em suas extremidades,
esferas com cargas elétricas de módulos iguais e sinais opostos. A barra A é
fixa, mas a barra B pode girar livremente em torno de seu centro O, que
permanece fixo. Nas situações I e II, a barra B foi colocada em equilíbrio, em
posições opostas. Para cada uma dessas duas situações, o equilíbrio da barra B
pode ser considerado como sendo, respectivamente.
(SITUAÇÕES DE EQUILÍBRIO - após o
sistema ser levemente deslocado de sua posição inicial
Estável = tende a retornar ao
equilíbrio inicial
Instável = tende a afastar-se do
equilíbrio inicial
Indiferente = permanece em
equilíbrio na nova posição)
a) indiferente e instável b) instável e instável c) estável e indiferente
d) estável e estável e) estável e instável
47) (UNIFESP) Considere a
seguinte "unidade" de medida: a intensidade da força elétrica entre
duas cargas q, quando separadas por uma distância d, é F. Suponha em seguida
que uma carga q1 = q seja colocada frente a duas outras cargas, q2
= 3q e q3 = 4q, segundo a disposição mostrada na figura.
A intensidade da força elétrica resultante
sobre a carga q1, devido às cargas q2 e q3,
será a) 2F. b) 3F. c) 4F. d) 5F. e) 9F.
48) (PUCRIO) Duas esferas idênticas, carregadas com cargas Q = 30 μ
C, estão suspensas a partir de um mesmo ponto por dois fios isolantes de mesmo
comprimento como mostra a figura.
Em equilíbrio, o ângulo Ɵ, formado
pelos dois fios isolantes com a vertical, é 45°. Sabendo que a massa de cada
esfera é de 1 kg, que a Constante de Coulomb é k = 9 × 109 N m2/C2
e que a aceleração da gravidade é g = 10 m/s2, determine a distância
entre as duas esferas quando em equilíbrio.
Lembre-se de que μ = 10-6.
a) 1,0 m b) 0,9 m c) 0,8 m d) 0,7 m e) 0,6 m
49) (UFPE) Quatro cargas
elétricas puntiformes, de intensidades Q e q, estão fixas nos vértices de um
quadrado, conforme indicado na figura. Determine a razão Q/q para que a força
sobre cada uma das cargas Q seja nula.
a) -√2/4 b) -√2/2 c) -√2 d) -2√2
e) -4√2
50) (UFRJ) Duas cargas
puntiformes q = 2,0 × 10-6 C e q‚ = 1,0 × 10-6C estão
fixas num plano nas posições dadas pelas coordenadas cartesianas indicadas a
seguir. Considere K = 1/(4 πɛ0) = 9,0 × 109 NC-2
m2.
Calcule o vetor
campo elétrico na posição A indicada na figura, explicitando seu módulo, sua
direção e seu sentido.
GABARITOS:
01) a) 6,0 m/s2, no sentido oposto ao
do movimento
b) 4,8 . 103 N, no sentido
oposto ao do movimento
02) A
03a) Observe a
figura a seguir:
b) 100 N c) 0,45
04) C
05) μ = 1 - 2√2/3 =
0,057
06) a) Observe a
figura a seguir:
b) 16 N
07) a) 2,5 N b) √3/6
08) E
09) B
10) B
11) C
12) D
13) A
14) C
15) B
16) a) maior que 7,3 rad/s b)
menor que 0,14 m
17) a) 75 N
b) 100 N
18) E
19) a) 200 J
b) 8,0 N
20) a) - 10 m/s
b) - 47,5 J
21) a) sen α > 1/N b)
sen ϕ < √(N2 - 1)
22) a) I - reflexão, II – refração b) N > √2
23) a) Reflexão e
Refração
b) Observe o esquema a seguir:
24) a) 45°
b) nprisma > 2
25) a) Entre o objeto e a imagem, a 80 cm do
objeto b) +16 cm
26)
a) Observe a figura a seguir:
b) 3f/4
27) Tendo em vista que os raios saem paralelos,
concluímos que eles estão incidindo no foco F.
A distância é igual a altura do triângulo eqüilátero ABF, ou seja 10√3
cm.
28) B
29) E
30) C
31)
8,0 mm
32) E
33) E
34) a) O defeito A é miopia e o defeito B pode
ser hipermetropia ou presbiopia
(vista cansada). O defeito A é corrigido pela lente 2, enquanto o defeito B é
corrigido pela lente 1.
b) O grau da lente 2 é D = - 2 di
35) C
36) a) 2,2 cm e 2,4 cm
b) Aproximadamente, 0,2 cm
"atrás" da retina
37) C
38) E
39) D
40) C
41) a) Polegar: intensidade de corrente elétrica.
Indicador: direção e sentido do vetor
campo magnético.
b) As linhas de indução magnética
formadas por um fio infinito, transportando corrente elétrica, são círculos
concêntricos ao fio.
c) O módulo do vetor campo magnético é
diretamente proporcional à intensidade de corrente elétrica e inversamente
proporcional à distância em que se encontra o fio.
42) B
43)
a)
b) 6,2 g
44)
a) Horário. Observe
a figura a seguir.
b) diminui
45) D
46) E
47) D
48) B
49) D
50|EA| =
9√5 × 107 N/C
Direção: tgα = |E2|/|E|
= 1/2, onde α é o ângulo trigonométrico que EA faz com o eixo 0x.
Sentido: de
afastamento da origem, a partir do ponto A










































Nenhum comentário:
Postar um comentário