LISTA DE EXERCÍCIOS - CICLO 3 - CADERNO
6
1)
(UNIFESP) Uma
pessoa de 70 kg desloca-se do andar térreo ao andar superior de uma grande loja
de departamentos, utilizando uma escada rolante. A figura fornece a velocidade e
a inclinação da escada em relação ao piso horizontal da
loja.

Considerando
que a pessoa permaneça sempre sobre o mesmo degrau da escada, e sendo g = 10
m/s2, sen 30°=
0,50 e cos 30°= 0,87, pode-se dizer que a energia transferida à pessoa por
unidade de tempo pela escada rolante durante esse percurso foi de:
a) 1,4 × 102 J/s. b)
2,1 × 102 J/s. c)
2,4 × 102 J/s. d) 3,7 ×
102 J/s. e)
5,0 × 102 J/s.
2)
(PUCPR)
Uma menina desce, a partir do repouso, o "Toboágua
Insano", com aproximadamente 40 metros de altura, e mergulha numa piscina
instalada em sua base. Usando g = 10 m/s2 e
supondo que o atrito ao longo do percurso dissipe 28% da energia mecânica,
calcule a velocidade da menina na base do toboágua.
Indique
o valor correto numa das alternativas a seguir: a) 70,2 km/h b)
86,4 km/h c) 62,5 km/h d) 90,0 km/h e) 100 km/h
3)
(FGV)
Devido a forças dissipativas, parte da energia
mecânica de um sistema foi convertida em calor, circunstância caracterizada pelo
gráfico apresentado.
Sabendo-se
que a variação da energia potencial desse sistema foi nula, o trabalho realizado
sobre o sistema nos primeiros 4 segundos, em J, foi, em módulo, a) 3
600. b) 1 200. c) 900. d) 800. e) 600.
4)
(UNICAMP) No
episódio II do filme Guerra nas Estrelas, um personagem mergulha em queda livre,
caindo em uma nave que se deslocava horizontalmente a 100 m/s com os motores
desligados. O personagem resgatado chegou à nave com uma velocidade de 6 m/s na vertical. Considere que a massa da nave é de 650 kg,
a do personagem resgatado de 80 kg e a do piloto de 70 kg.
a) Quais
as componentes horizontal e vertical da velocidade da nave imediatamente após o
resgate?
b) Qual
foi a variação da energia cinética total nesse
resgate?
5)
(UNESP) Um
veículo está rodando à velocidade de 36 km/h numa estrada reta e horizontal,
quando o motorista aciona o freio. Supondo que a velocidade do veículo se reduz
uniformemente à razão de 4 m/s em cada segundo a partir do momento em que o
freio foi acionado, determine
a) o
tempo decorrido entre o instante do acionamento do freio e o instante em que o
veículo pára.
b) a
distância percorrida pelo veículo nesse intervalo de
tempo.
6)
(PUCSP) Uma
criança de massa 25 kg, inicialmente no ponto A, distante 2,4 m do solo,
percorre, a partir do repouso, o escorregador esquematizado na figura. O
escorregador pode ser considerado um plano inclinado cujo ângulo com a
horizontal é de 37°. Supondo o coeficiente de atrito cinético entre a roupa da
criança e o escorregador igual a 0,5, a velocidade com que a criança chega à
base do escorregador (ponto B) é, em m/s,
Dados: sen 37° = 0,6; cos 37° = 0,8; tg 37° =
0,75
7)
(UNESP) Um
projétil de 20 gramas, com velocidade de 240m/s, atinge o tronco de uma árvore e
nele penetra uma certa distância até parar.
a)
Determine a energia cinética Ec do projétil antes de
colidir com o tronco e o trabalho T realizado sobre o projétil na sua trajetória
no interior do tronco, até parar.
b)
Sabendo que o projétil penetrou 18cm no tronco da árvore, determine o valor
médio Fm da força de resistência que o tronco ofereceu à penetração do
projétil.
8)
(UNESP) Uma
esfera de aço de massa 0,20kg é abandonada de uma altura de 5,0m, atinge o solo
e volta, alcançando a altura máxima de 1,8m. Despreze a resistência do ar e
suponha que o choque da esfera com o solo ocorra durante um intervalo de tempo
de 0,050s. Levando em conta esse intervalo de tempo,
determine:
a) a
perda de energia mecânica
b) a força média exercida pelo solo sobre a
esfera. Adote g = 10 m/s2.
9)
(UNICAMP) A tração
animal pode ter sido a primeira fonte externa de energia usada pelo homem e
representa um aspecto marcante da sua relação com os
animais.
a) O
gráfico mostra a força de tração exercida por um cavalo como função do
deslocamento de uma carroça. O trabalho realizado pela força é dado pela área
sob a curva F × d. Calcule o trabalho realizado pela força de tração do cavalo
na região em que ela é constante.
b) No
sistema internacional, a unidade de potência é o watt (W) = 1 J/s. O uso de
tração animal era tão difundido no passado que James Watt, aprimorador da máquina a vapor, definiu uma unidade de
potência tomando os cavalos como referência. O cavalo vapor (CV), definido a partir da ideia de
Watt, vale aproximadamente 740 W. Suponha que um cavalo, transportando uma
pessoa ao longo do dia, realize um trabalho total de 444000 J. Sabendo que o
motor de uma moto,operando na potência máxima,executa esse mesmo trabalho em
40s, calcule a potência máxima do motor da moto em CV.
10)
(FUVEST) A usina
hidrelétrica de Itaipu possui 20 turbinas, cada uma fornecendo uma potência
elétrica útil de 680 MW, a partir de um desnível de água de 120 m. No complexo,
construído no Rio Paraná, as águas da represa passam em cada turbina com vazão
de 600 m3/s.
a)
Estime o número de domicílios, N, que deixariam de ser atendidos se, pela queda
de um raio, uma dessas turbinas interrompesse sua operação entre 17 h 30 min e
20 h 30 min, considerando que o consumo médio de energia, por domicílio, nesse
período, seja de 4 kWh.
b)
Estime a massa M, em kg, de água do rio que entra em cada turbina, a cada
segundo.
c)
Estime a potência mecânica da água P, em MW, em cada
turbina.
NOTE E
ADOTE:
Densidade
da água = 103 kg/m3. 1 MW = 1 megawatt = 106
W.
1 kWh =
1000 W . 3600 s = 3,6 . 106J.
Os
valores mencionados foram aproximados para facilitar os
cálculos.
11)
(FUVEST) Um
elevador de carga, com massa M = 5 000 kg, é suspenso por um cabo na parte
externa de um edifício em construção. Nas condições das questões a seguir,
considere que o motor fornece a potência P = 150 kW.
a)
Determine a força F, em N, que o cabo exerce sobre o elevador, quando ele é
puxado com velocidade constante.
b)
Determine a força F2, em N, que o cabo exerce sobre o elevador, no
instante em que ele está subindo com uma aceleração para cima de módulo a = 5
m/s2.
c)
Levando em conta a potência P do motor, determine a velocidade V2, em
m/s, com que o elevador estará subindo, nas condições do item (b) (a = 5
m/s2).
d)
Determine a velocidade máxima VL, em m/s, com que o elevador pode subir quando
puxado pelo motor.
NOTE E
ADOTE:
A
potência P, desenvolvida por uma força F, é igual ao produto da força pela
velocidade V do corpo em que atua, quando V tem a direção e o sentido da
força.
12) (UNESP) O teste Margaria de corrida em
escada é um meio rápido de medida de potência anaeróbica de uma pessoa. Consiste
em fazê-la subir uma escada de dois em dois degraus, cada um com 18 cm de
altura, partindo com velocidade máxima e constante de uma distância de alguns
metros da escada. Quando pisa no 8º. degrau, a pessoa aciona um cronômetro, que
se desliga quando pisa no 12º. degrau. Se o intervalo de tempo registrado para
uma pessoa de 70 kg foi de 2,8 s e considerando a aceleração da gravidade igual
a 10 m/s2, a potência média
avaliada por este método foi de:
a) 180 W. b) 220 W. c) 432 W. d) 500 W. e) 644 W.
13)
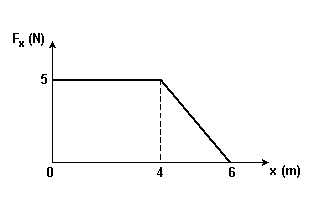
(UFPEL) Um corpo
de massa m se move ao longo do eixo x sob a ação de uma força ù, cujo módulo é
representado no gráfico a seguir, em função do módulo do deslocamento. Tanto a
força F quanto o deslocamento x possuem a mesma direção e o mesmo
sentido.
A partir
da análise do gráfico, pode-se afirmar que o trabalho realizado pela força ao
deslocar o corpo desde a origem até a posição x' é
14)
(UNESP) A
relação entre calor e outras formas de energia foi objeto de intensos estudos
durante a Revolução Industrial, e uma experiência realizada por James P. Joule
foi imortalizada. Com ela, ficou demonstrado que o trabalho mecânico e o calor
são duas formas diferentes de energia e que o trabalho mecânico poderia ser
convertido em energia térmica. A figura apresenta uma versão atualizada da
máquina de Joule. Um corpo de massa 2 kg é suspenso por um fio cuidadosamente
enrolado em um carretel, ligado ao eixo de um gerador.
O
gerador converte a energia mecânica do corpo em elétrica e alimenta um resistor
imerso em um recipiente com água. Suponha que, até que o corpo chegue ao solo,
depois de abandonado a partir do repouso, sejam transferidos para a água 24 J de
energia térmica. Sabendo que esse valor corresponde a 80% da energia mecânica,
de qual altura em relação ao solo o corpo foi abandonado? Adote g = 10
m/s2.
15)
(UNIFESP)
A figura representa o gráfico do módulo F de uma força que atua sobre um corpo
em função do seu deslocamento x. Sabe-se que a força atua sempre na mesma
direção e sentido do deslocamento.
Pode-se
afirmar que o trabalho dessa força no trecho representado pelo gráfico é, em
joules,
a)
0. b) 2,5. c) 5,0. d) 7,5. e) 10.
16)
(UNESP) Uma
força atuando em uma caixa varia com a distância x de acordo com o
gráfico.
O
trabalho realizado por essa força para mover a caixa da posição x = 0 até a
posição x = 6 m vale
a) 5
J. b) 15 J. c) 20 J. d) 25 J. e) 30 J.
17)
(UFMG) Um
bloco de massa 0,20 kg desce deslizando sobre a superfície mostrada na figura a
seguir.
No ponto
A, a 60 cm acima do plano horizontal EBC, o bloco tem uma velocidade de 2,0 m/s
e, ao passar pelo ponto B, sua velocidade é de 3,0 m/s. Considere g = 10
m/s2.
1 -
Mostre, usando idéias relacionadas ao conceito de energia, que, entre os pontos
A e B, existe atrito entre o bloco e a superfície.
2 -
Determine o trabalho realizado pela força de atrito que atua no bloco entre os
pontos A e B.
3 -
Determine o valor do coeficiente de atrito entre a superfície horizontal e o
bloco, sabendo-se que ele chega ao repouso no ponto C, distante 90 cm de
B.
18)
(UNESP) Uma
preguiça de massa 1,2kg desprende-se do galho de uma árvore, à beira de um
penhasco, e cai verticalmente. Sua velocidade cresce até 42m/s, quando se torna
constante, devido à resistência do ar.
a)
Considerando g = 10m/s2, calcule a intensidade máxima da força de
resistência do ar.
b)
Em seguida, felizmente, a preguiça cai sobre uma vegetação arbustiva, que
amortece a queda, parando-a completamente. Calcule a quantidade de energia
mecânica dissipada na interação da preguiça com a vegetação. (Despreze o
trabalho realizado pela força peso durante o freamento
na vegetação.)
19)
(UEL) Um
corpo de massa m=0,50kg desliza por uma pista inclinada, passando pelo ponto A
com velocidade VA=2,0m/s e pelo ponto B com velocidade
VB=6,0m/s. Adote g=10m/s2.
20)
(UNESP) Um
corpo cai em queda livre, a partir do repouso, sob ação da gravidade. Se sua
velocidade, depois de perder uma quantidade E de energia potencial
gravitacional, é v, podemos concluir que a massa do corpo é dada
por
a)
2Ev. b) 2E/v2. c) 2Ev2. d) √(2Ev). e)
2v2/E.
21)
(UFPR) Um
observador parado vê uma pessoa dar uma pancada num sino situado a 680 m. Após
um intervalo de tempo ∆t ele escuta um som de freqüência 85,0 Hz. Supondo que o
ar esteja em repouso e que a velocidade do som seja de 340 m/s, é correto
afirmar que:
(01) O
intervalo de tempo ∆t é igual a 2,00 s.
(02)
Para um som de freqüência 850 Hz, ∆t seria igual a 0,20 s.
(04) A
distância do observador ao sino contém 170 comprimentos de
onda.
(08) Se,
no momento em que escutou o som, o observador estivesse correndo em direção ao
sino, ele ouviria um som mais agudo.
(16) Se
o sino e o observador estivessem em margens opostas de um lago, e o observador
tivesse a orelha esquerda dentro da água e a direita no ar, haveria um intervalo
de tempo entre os sons recebidos em cada ouvido.
Soma =
(
)
22)
(MACKENZIE)
A figura a seguir ilustra uma onda mecânica que se propaga numa velocidade 3,0
m/s. A frequência é:
a)
1,5 Hz. b) 3,0 Hz. c) 5,0 Hz. d) 6,0 Hz. e) 10,0 Hz.
23)
(FUVEST) Uma
fonte emite ondas sonoras de 200 Hz. A uma distância de 3400 m da fonte está
instalado um aparelho que registra a chegada das ondas através do ar e as remete
de volta através de um fio metálico retilíneo. O comprimento dessas ondas no fio
é 17 m. Qual o tempo de ida e volta das ondas?
Dado: velocidade do som no ar = 340 m/s
a) 11 s b) 17 s c) 22 s d) 34 s e) 200 s
24)
(FUVEST) Uma
roda, contendo em sua borda 20 dentes regularmente espaçados, gira uniformemente
dando 5 voltas por segundo. Seus dentes se chocam com uma palheta produzindo
sons que se propagam a 340 m/s.
a) Qual
a freqüência do som produzido?
b) Qual
o comprimento de onda do som produzido?
25)
(FUVEST) Uma
bóia pode se deslocar livremente ao longo de uma haste vertical, fixada no fundo
do mar. Na figura, a curva cheia representa uma onda no instante t = 0s e a
curva tracejada a mesma onda no instante t = 0,2s. Com a passagem dessa onda, a
bóia oscila.
Nesta
situação, o menor valor possível da velocidade da onda e o correspondente
período de oscilação da bóia, valem: a) 2,5 m/s e 0,2 s b) 5,0 m/s e 0,4 s c) 0,5 m/s e 0,2 s d) 5,0 m/s e 0,8 s
e) 2,5
m/s e 0,8 s
26)
(UNESP) A
figura reproduz duas fotografias instantâneas de uma onda que se deslocou para a
direita numa corda.
a) Qual
é o comprimento de onda dessa onda?
b)
Sabendo-se que, no intervalo de tempo entre as duas fotos, 1/10s, a onda se
deslocou menos que um comprimento de onda, determine a velocidade de propagação
e a freqüência dessa onda.
27)
(FUVEST) Um
trecho dos trilhos de aço de uma ferrovia tem a forma e as dimensões dadas a
seguir. Um operário bate com uma marreta no ponto A dos trilhos. Um outro
trabalhador, localizado no ponto B, pode ver o primeiro, ouvir o ruído e sentir
com os pés as vibrações produzidas pelas marretadas no
trilho.
a)
supondo que a luz se propague instantaneamente, qual o intervalo de tempo ∆t
decorrido entre os instantes em que o trabalhador em B vê uma marretada e ouve o
seu som?
b) Qual
a velocidade de propagação do som no aço, sabendo-se que o trabalhador em B, ao
ouvir uma marretada, sente simultaneamente as vibrações no
trilho?
Dado: a
velocidade do som no ar é de 340 m/s. Para fazer as contas use π =
3.
28)
(UNESP) O
caráter ondulatório do som pode ser utilizado para eliminação, total ou parcial,
de ruídos indesejáveis. Para isso, microfones captam o ruído do ambiente e o
enviam a um computador, programado para analisá-lo e para emitir um sinal
ondulatório que anule o ruído original indesejável. O fenômeno ondulatório no
qual se fundamenta essa nova tecnologia é a:
a)
interferência b) difração c) polarização d) reflexão e) refração
29)
(UEL) Considere
as afirmações a seguir.
I. O
fenômeno de interferência reforça o caráter ondulatório da
luz.
II. A
reflexão do som tem características semelhantes à reflexão da
luz.
III.
Ondas podem sofrer refração.
Pode-se
afirmar que
a)
somente I é correta b) somente II é correta c) somente III é
correta
d)
somente I e II são corretas e) I, II e III são
corretas
30)
(UNIRIO) Um
movimento ondulatório propaga-se para a direita e encontra o obstáculo AB, onde
ocorre o fenômeno representado na figura a seguir, que é o de:
a)
difração b) difusão
c) dispersão d) refração
e)
polarização
31)
(MACKENZIE) Uma
corda feita de um material, cuja densidade linear é 10 g/m, está sob tensão
provocada por uma força de 900 N. Os suportes fixos distam de 90 cm. Faz-se
vibrar a corda transversalmente e esta produz ondas estacionárias, representadas
na figura a seguir. A freqüência das ondas componentes, cuja superposição causa
esta vibração, é;
a)
100 Hz b) 200 Hz
c) 300 Hz
d) 400 Hz e) 500 Hz
32)
(UFRJ) Um
artesão constrói um instrumento musical rústico usando cordas presas a dois
travessões. As cordas são todas de mesmo material, de mesmo diâmetro e
submetidas à mesma tensão, de modo que a velocidade com que nelas se propagam
ondas transversais seja a mesma. Para que o instrumento possa emitir as diversas
notas musicais, ele utiliza cordas de comprimentos diferentes, como mostra a
figura.
Uma
vez afinado o instrumento, suponha que cada corda vibre em sua frequência
fundamental.
Que
corda emite o som mais grave, a mais longa ou a mais curta? Justifique sua
resposta.
33)
(UFRJ) Uma
corda de violão é posta a vibrar e são obtidos sucessivamente os dois estados
estacionários ilustrados nas figuras a seguir.
Calcule
a razão f1/f2 entre a freqüência f1 do estado
estacionário 1 e a freqüência f2 do estado estacionário
2.
34)
(FUVEST) O comandante de um jumbo decide elevar a
altitude de vôo do avião de 9000 m para 11000 m. Com relação à anterior, nesta
2ª altitude:
a) a
distância do vôo será menor.
b) o
empuxo que o ar exerce sobre o avião será maior.
c) a
densidade do ar será menor.
d) a
temperatura externa será maior.
e) a
pressão atmosférica será maior.
35)
(FATEC) Um
tapete pesando 75N tem dimensões 2,5m × 2,0m. Adotando-se g=10m/s2, a
densidade superficial do tapete, em kg/m2, é: a) 0,067 b) 0,15
c) 0,67 d) 1,5 e) 15
36)
(UNESP) Um
tijolo, com as dimensões indicadas, é colocado sobre uma mesa com tampo de
borracha, inicialmente da maneira mostrada em 1 e, posteriormente, da maneira
mostrada em 2.
Na
situação 1, o tijolo exerce sobre a mesa uma força F1 e uma pressão
p1; na situação 2, a força e a pressão exercidas são F2 e
p2.
Nessas
condições, pode-se afirmar que:
a)
F1 = F2 e p1 = p2 b) F1 =
F2 e p1 > p2 c) F1 =
F2 e p1 < p2
d)
F1 > F2 e p1 > p2 e) F1 <
F2 e p1 < p2
37)
(UNICAMP) Um
mergulhador persegue um peixe a 5,0 m abaixo da superfície de um lago. O peixe
foge da posição A e se esconde em uma gruta na posição B, conforme mostra a
figura a seguir. A pressão atmosférica na superfície da água é igual a
P0 = 1,0.105 N/m2. Adote g = 10
m/s2.
a) Qual
a pressão sobre o mergulhador?
b) Qual
a variação de pressão sobre o peixe nas posições A e B?
38)
(UNICAMP) Partículas
α (núcleo de um átomo de Hélio), partículas β (elétrons) e radiação γ (onda
eletromagnética) penetram, com velocidades comparáveis, perpendicularmente a um
campo elétrico uniforme existente numa região do espaço, descrevendo as
trajetórias esquematizadas na figura a seguir.
a)
Reproduza a figura anterior e associe α, β e γ a cada uma das três
trajetórias.
b) Qual
é o sentido do campo elétrico?
39)
(UNICAMP)
Uma molécula diatômica tem átomos com carga + q e - q. A distância entre os
átomos é d. A molécula está numa região onde existe um campo elétrico uniforme
E.Indique em qual das seguintes posições a molécula estará em equilíbrio
estável. Justifique.
40)
(UEL) A
diferença de potencial entre duas placas condutoras paralelas, representadas no
esquema a seguir, é 200 volts. Considerando as indicações do esquema, a
diferença de potencial entre os pontos P1 e P2, em volts,
é igual
a)
40 b)
50 c)
110 d)
160 e) 200
41)
(UNICAMP) Considere
uma esfera de massa m e carga q pendurada no teto e sob a ação da gravidade e do
campo elétrico E como indicado na figura a seguir.
a) Qual
é o sinal da carga q? Justifique sua resposta.
b) Qual
é o valor do ângulo Ɵ no equilíbrio?
42)
(MACKENZIE) Num
ponto A do universo, constata-se a existência de um campo elétrico û de
intensidade 9,0.105N/C, devido exclusivamente a uma carga puntiforme
Q situada a 10cm dele. Num outro ponto B, distante 30cm da mesma carga, o vetor
campo elétrico tem intensidade 1,0.105N/C. A d.d.p. entre A e B
é: a) 8,0.105
V b) 6,0.105 V c) 6,0.104 V d) 2,0.104 V e) 1,8.104
V
43)
(MACKENZIE) Uma
partícula de 1,0g está eletrizada com carga 1,0μC. Ao ser abandonada do repouso,
no ponto A do campo elétrico da carga puntiforme Q, fica sujeita a uma força
elétrica cujo trabalho por ela realizado, entre este ponto A e o ponto B, é
igual ao trabalho realizado pelo seu próprio peso, durante sua queda num
desnível de 40m. Sabendo-se que
k0=9.109N.m2/C2 e que
g=10m/s2, podemos afirmar que o valor da carga Q é: a) 1,0 μC b) 2,0 μC c) 3,0 μC d) 4,0 μC e) 5,0 μC
44)
(MACKENZIE) A 40
cm de um corpúsculo eletrizado, coloca-se uma carga puntiforme de 2,0 μC. Nessa
posição, a carga adquire energia potencial elétrica igual a 0,54 J.
Considerando
k0 = 9 109 Nm2/C2, a carga elétrica
do corpúsculo eletrizado é:
a) 20
μC b) 12 μC c) 9 μC d) 6 μC e) 4 Μc
GABARITOS:
01) B
02) B
03) B
04) a) Vx = 90m/s Vy =
0,6m/s b) - 3,6 ×
105J
05) a) 2,5 s b) 12,5 m
06) D
07) a) Ec = 576 J e T = -
576 J b) Fm = 3,2 . 103
N
08) a) 6,4J e
b) 66,0 N
09) a) Trabalho =
32000J b) 15
CV
10) a) N =
510000. b) M = 600000 kg. c) P = 720 MW.
11) a) 5,0 ×
104N b) 7,5 ×
104N c) 2,0m/s d) 3,0m/s
12)
A
13)
A
14) h = 1,5
m
15)
C
16)
D
17) 1 - ∆ɛ = ɛB - ɛA
= 0,9 - 1,6 = - 0,70 J. Existe atrito.
2 - 0,70 J.
3- μ= 0,50.
18) a) 12 N b) 1,06 kJ
19)
D
20)
B
21) 01 + 04 + 08
+ 16 = 29
22)
E
23)
A
24) a) f = 100
Hz b) λ = 3,4
m
25)
E
26) a) 40 cm b) 2,0 m/s e 5,0 Hz
27) a) 1,5 s b) 4910 m/s
28)
A
29)
E
30)
A
31)
E
32) Som mais
grave possui a menor freqüência.
- freqüência numa
corda sonora: f = nv/2ℓ
onde ℓ =
comprimento da corda.
- para a
freqüência fundamental; n=1; f=1/2v/ℓ
- logo f é
inversamente proporcional a Ø.ℓ
Assim f será
mínima quando ℓ for máximo.
portanto, A corda
de MAIOR comprimento emite o som MAIS GRAVE.
33)
f1/f2 = 1/3
34)
C
35)
D
36)
C
37) a) 1,5 .
105 N/m2 b)
zero
38)
b) Da placa B para a placa
A.
39) Posição
d
40)
C
41) a) O esquema
a seguir mostra as forças atuantes na esfera:
T = tração
aplicada pelo fio, P = peso aplicado
pela Terra,
Fe = Força
elétrica devida ao campo elétrico E
O sinal da carga
é negativo, pois, devido à geometria do sistema, conclui-se que a força elétrica
tem sentido oposto ao do campo.
b) Ɵ = arctg (|q|.E)/10m
(SI)
42)
C
43)
B
44)
B



























Nenhum comentário:
Postar um comentário